PROMPT
Identify two readings from the course reading list that relate to your investigation, and then describe and expand on these connections through writing. To help you be specific, describe the connection to each reading in context of one of the following types of relationship.
(theme, form, process)

I selected the bridge tunnel beneath Regent’s Canal as my research investigating. My overall investigative approach drew from Georges Perec’s observational methodology outlined in ‘Notes on a work in progress’ (Perec, 1974, p. 56), particularly his concept of the ‘time capsule’ (Perec, 1974, p. 56) and its temporal framework. This methodological approach resonated with my intended investigation of the ‘space-time tunnel’, inspiring an exploration of the temporal dimensions within the Regent’s Canal bridge tunnel. Additionally, I incorporated Perec’s systematic observational concepts, such as the ‘orthogonal Latin bi-square, this time of order 12’ (Perec, 1974, p. 56). However, acknowledging the practical limitations of conducting a 12-year continuous observation as Perec did, I reconsidered the systematic framework.

In developing my systematic approach, I explored the possibility of integrating graphic design language with systematic observation methods. Drawing from John Cage’s ‘Chance Operations’ (Jensen, 2009), I established a graphic design grid system using individual stone slabs as the foundational framework. Within this structure, I incorporated Villard de Honnecourt’s ‘Euclidean Geometry’ (Zenner, 2002) for graphic grid system design, alongside established design principles such as ‘The Grid and Golden Ratio’. However, during implementation, I discovered that Villard de Honnecourt’s approach proved excessively rational and pristine, failing to accommodate the dynamic variations of actual field conditions. This realization necessitated a transformation of my observational methodology.

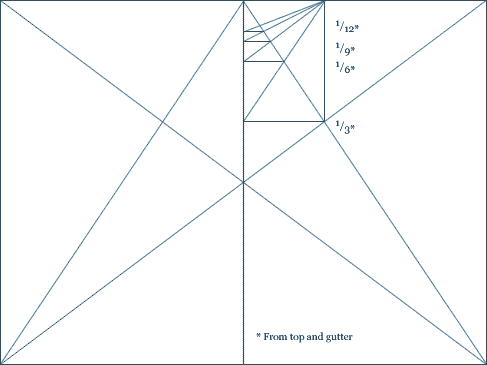
In the final methodology, I addressed the challenge of translating 3D states into 2D language. To resolve this issue, I implemented a ‘Projected Coordinate System’ (Kennedy, 2009). I established the trajectory between the observation point’s latitude and longitude as the ‘principal axis’, then connected this principal axis with the ‘true north’ axis to derive angle θ, which became my fixed observational angle.

I aim to conduct a more granular and comprehensive observation of a spatial environment, rather than relying solely on surface-level methods. As McLuhan notes in ‘The Medium is the Massage’, ‘Environments are not passive wrappings, but are, rather, active processes which are invisible’ (McLuhan & FIORE, 2001, p. 38). Motivated by this insight, I seek to probe further; and to ensure that observers other than myself can readily employ the method, I have devised a comprehensive observation protocol. Observers may determine their coordinate system on the basis of the ‘Mercator projection’ (Mercator, 1569), thereby calculating their position within the grid. The protocol includes:

·Observer coordinates

·‘Projected Coordinate System’ (Kennedy, 2009)

·Specific events occurring within 10-minute intervals

·Detailed observational information, including whether observed subjects deviated from the principal axis trajectory

Subsequently, I calculated the ‘Projected Coordinate System’ (Kennedy, 2009) of latitude and longitude using the ‘Mercator projection’ (Mercator, 1569). Through specific X-Y values, I reconstructed the observational grid and plotted my coordinates within this framework. Ultimately, I achieved a grid system that successfully translates three-dimensional space into graphic design language.

Following this systematic approach, I meticulously documented individual bricks beneath the bridge tunnel, mapping their shapes and gap intervals onto the grid system. This investigation seeks to explore the dialectic between ‘rules’ and ‘nature’, which constitutes the core inquiry of this research project.